This method computes the gradients (also known as Vanilla Gradients) of
the outputs with respect to the input variables, i.e., for all input
variable \(i\) and output class \(j\)
$$d f(x)_j / d x_i.$$
If the argument times_input is TRUE, the gradients are multiplied by
the respective input value (Gradient\(\times\)Input), i.e.,
$$x_i * d f(x)_j / d x_i.$$
While the vanilla gradients emphasize prediction-sensitive features,
Gradient\(\times\)Input is a decomposition of the output into feature-wise
effects based on the first-order Taylor decomposition.
The R6 class can also be initialized using the run_grad function as a
helper function so that no prior knowledge of R6 classes is required.
See also
Other methods:
ConnectionWeights,
DeepLift,
DeepSHAP,
ExpectedGradient,
IntegratedGradient,
LIME,
LRP,
SHAP,
SmoothGrad
Super classes
innsight::InterpretingMethod -> innsight::GradientBased -> Gradient
Methods
Method new()
Create a new instance of the Gradient R6 class. When initialized,
the method Gradient or Gradient\(\times\)Input is applied to the
given data and the results are stored in the field result.
Usage
Gradient$new(
converter,
data,
channels_first = TRUE,
output_idx = NULL,
output_label = NULL,
ignore_last_act = TRUE,
times_input = FALSE,
verbose = interactive(),
dtype = "float"
)Arguments
converter(
Converter)
An instance of theConverterclass that includes the torch-converted model and some other model-specific attributes. SeeConverterfor details.data(
array,data.frame,torch_tensororlist)
The data to which the method is to be applied. These must have the same format as the input data of the passed model to the converter object. This means eitheran
array,data.frame,torch_tensoror array-like format of size (batch_size, dim_in), if e.g., the model has only one input layer, ora
listwith the corresponding input data (according to the upper point) for each of the input layers.
channels_first(
logical(1))
The channel position of the given data (argumentdata). IfTRUE, the channel axis is placed at the second position between the batch size and the rest of the input axes, e.g.,c(10,3,32,32)for a batch of ten images with three channels and a height and width of 32 pixels. Otherwise (FALSE), the channel axis is at the last position, i.e.,c(10,32,32,3). If the data has no channel axis, use the default valueTRUE.output_idx(
integer,listorNULL)
These indices specify the output nodes for which the method is to be applied. In order to allow models with multiple output layers, there are the following possibilities to select the indices of the output nodes in the individual output layers:An
integervector of indices: If the model has only one output layer, the values correspond to the indices of the output nodes, e.g.,c(1,3,4)for the first, third and fourth output node. If there are multiple output layers, the indices of the output nodes from the first output layer are considered.A
listofintegervectors of indices: If the method is to be applied to output nodes from different layers, a list can be passed that specifies the desired indices of the output nodes for each output layer. Unwanted output layers have the entryNULLinstead of a vector of indices, e.g.,list(NULL, c(1,3))for the first and third output node in the second output layer.NULL(default): The method is applied to all output nodes in the first output layer but is limited to the first ten as the calculations become more computationally expensive for more output nodes.
output_label(
character,factor,listorNULL)
These values specify the output nodes for which the method is to be applied. Only values that were previously passed with the argumentoutput_namesin theconvertercan be used. In order to allow models with multiple output layers, there are the following possibilities to select the names of the output nodes in the individual output layers:A
charactervector orfactorof labels: If the model has only one output layer, the values correspond to the labels of the output nodes named in the passedConverterobject, e.g.,c("a", "c", "d")for the first, third and fourth output node if the output names arec("a", "b", "c", "d"). If there are multiple output layers, the names of the output nodes from the first output layer are considered.A
listofcharactor/factorvectors of labels: If the method is to be applied to output nodes from different layers, a list can be passed that specifies the desired labels of the output nodes for each output layer. Unwanted output layers have the entryNULLinstead of a vector of labels, e.g.,list(NULL, c("a", "c"))for the first and third output node in the second output layer.NULL(default): The method is applied to all output nodes in the first output layer but is limited to the first ten as the calculations become more computationally expensive for more output nodes.
ignore_last_act(
logical(1))
Set this logical value to include the last activation functions for each output layer, or not (default:TRUE). In practice, the last activation (especially for softmax activation) is often omitted.times_input(
logical(1))
Multiplies the gradients with the input features. This method is called Gradient\(\times\)Input.verbose(
logical(1))
This logical argument determines whether a progress bar is displayed for the calculation of the method or not. The default value is the output of the primitive R functioninteractive().dtype(
character(1))
The data type for the calculations. Use either'float'fortorch_floator'double'fortorch_double.
Examples
#----------------------- Example 1: Torch ----------------------------------
library(torch)
# Create nn_sequential model and data
model <- nn_sequential(
nn_linear(5, 12),
nn_relu(),
nn_linear(12, 2),
nn_softmax(dim = 2)
)
data <- torch_randn(25, 5)
# Create Converter with input and output names
converter <- convert(model,
input_dim = c(5),
input_names = list(c("Car", "Cat", "Dog", "Plane", "Horse")),
output_names = list(c("Buy it!", "Don't buy it!"))
)
# Calculate the Gradients
grad <- Gradient$new(converter, data)
# You can also use the helper function `run_grad` for initializing
# an R6 Gradient object
grad <- run_grad(converter, data)
# Print the result as a data.frame for first 5 rows
get_result(grad, "data.frame")[1:5,]
#> data model_input model_output feature output_node value pred
#> 1 data_1 Input_1 Output_1 Car Buy it! -0.14825179 0.4350947
#> 2 data_2 Input_1 Output_1 Car Buy it! 0.05937952 0.3516106
#> 3 data_3 Input_1 Output_1 Car Buy it! -0.11920095 0.3579636
#> 4 data_4 Input_1 Output_1 Car Buy it! 0.04680012 0.4330536
#> 5 data_5 Input_1 Output_1 Car Buy it! -0.10334471 0.4142854
#> decomp_sum decomp_goal input_dimension
#> 1 -0.4881209 -0.5611503 1
#> 2 -0.2868419 -0.4182229 1
#> 3 -0.5454712 -0.5449153 1
#> 4 -0.3517682 -0.3581279 1
#> 5 -0.2500831 -0.4560646 1
# Plot the result for both classes
plot(grad, output_idx = 1:2)
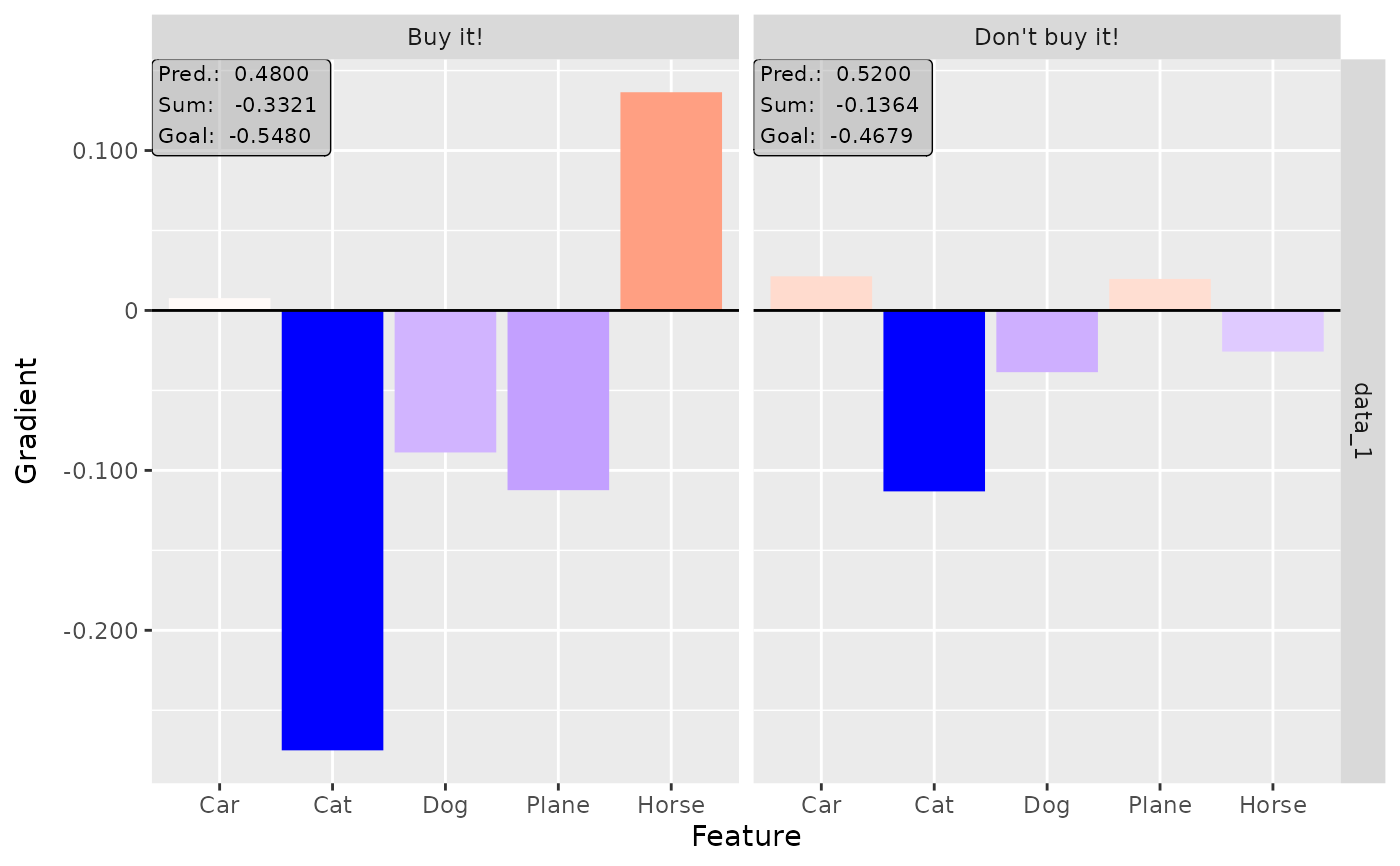 # Plot the boxplot of all datapoints
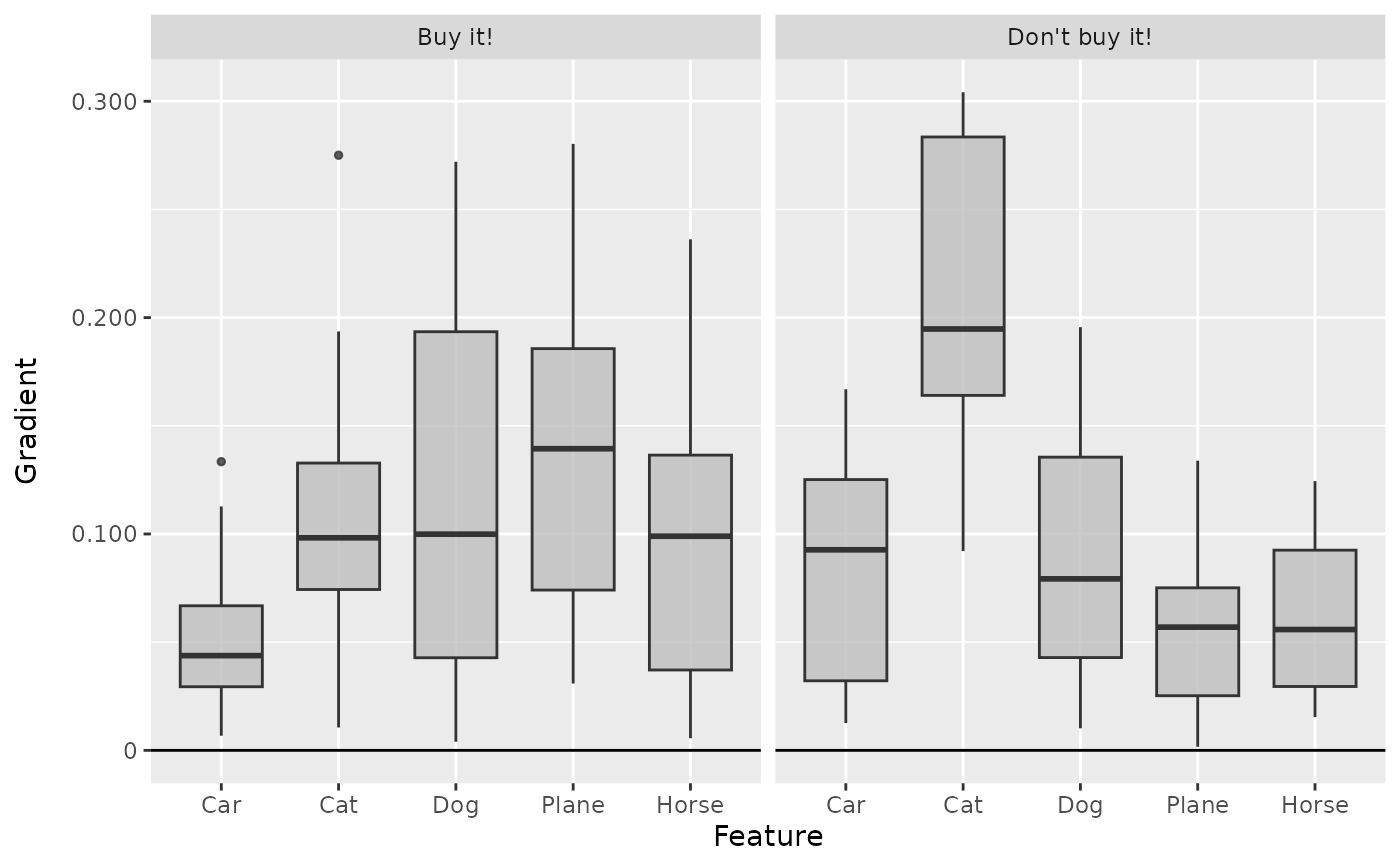
boxplot(grad, output_idx = 1:2)
# Plot the boxplot of all datapoints
boxplot(grad, output_idx = 1:2)
 # ------------------------- Example 2: Neuralnet ---------------------------
if (require("neuralnet")) {
library(neuralnet)
data(iris)
# Train a neural network
nn <- neuralnet(Species ~ ., iris,
linear.output = FALSE,
hidden = c(10, 5),
act.fct = "logistic",
rep = 1
)
# Convert the trained model
converter <- convert(nn)
# Calculate the gradients
gradient <- run_grad(converter, iris[, -5])
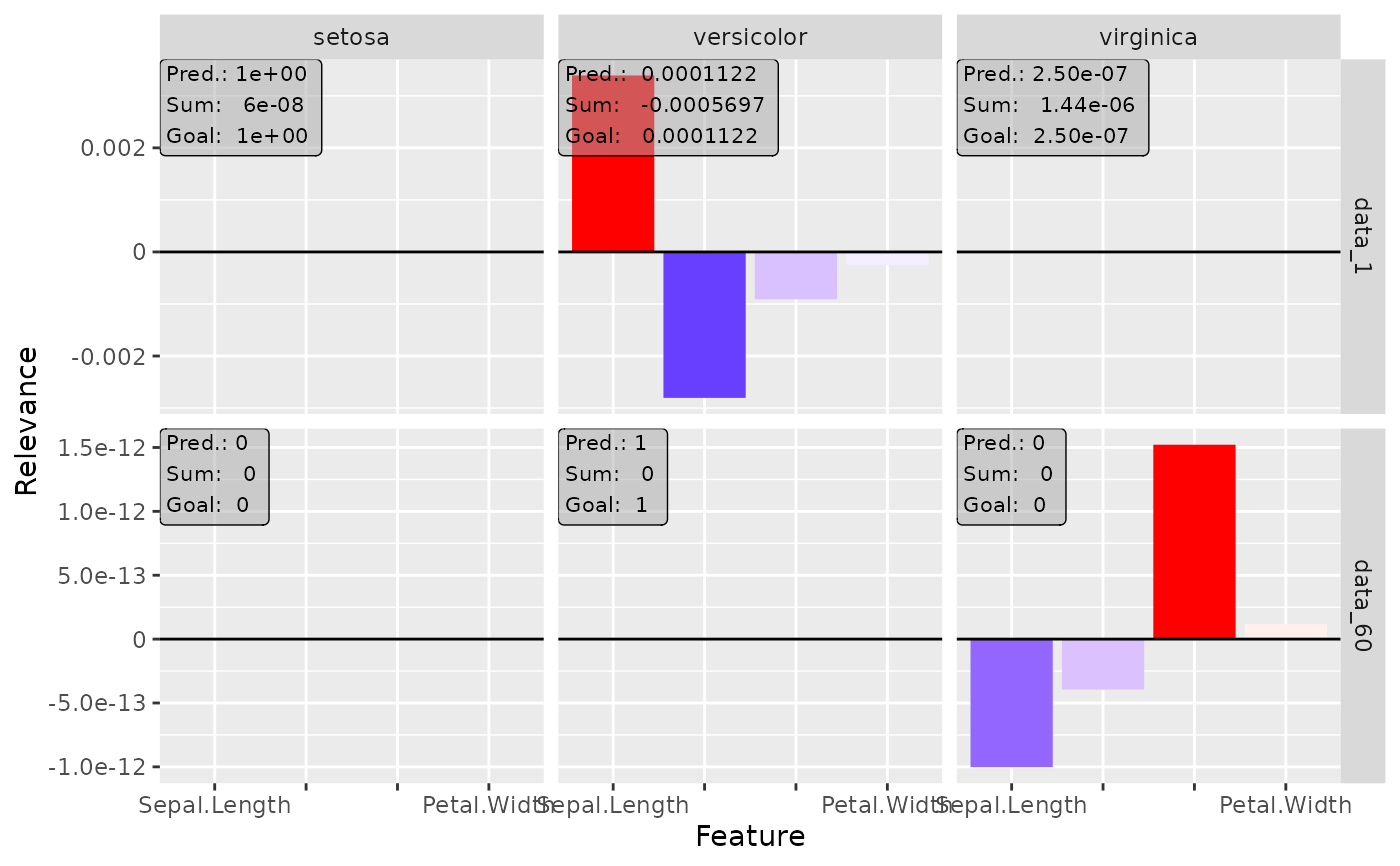
# Plot the result for the first and 60th data point and all classes
plot(gradient, data_idx = c(1, 60), output_idx = 1:3)
# Calculate Gradients x Input and do not ignore the last activation
gradient <- run_grad(converter, iris[, -5],
ignore_last_act = FALSE,
times_input = TRUE)
# Plot the result again
plot(gradient, data_idx = c(1, 60), output_idx = 1:3)
}
# ------------------------- Example 2: Neuralnet ---------------------------
if (require("neuralnet")) {
library(neuralnet)
data(iris)
# Train a neural network
nn <- neuralnet(Species ~ ., iris,
linear.output = FALSE,
hidden = c(10, 5),
act.fct = "logistic",
rep = 1
)
# Convert the trained model
converter <- convert(nn)
# Calculate the gradients
gradient <- run_grad(converter, iris[, -5])
# Plot the result for the first and 60th data point and all classes
plot(gradient, data_idx = c(1, 60), output_idx = 1:3)
# Calculate Gradients x Input and do not ignore the last activation
gradient <- run_grad(converter, iris[, -5],
ignore_last_act = FALSE,
times_input = TRUE)
# Plot the result again
plot(gradient, data_idx = c(1, 60), output_idx = 1:3)
}
 # ------------------------- Example 3: Keras -------------------------------
if (require("keras") & keras::is_keras_available()) {
library(keras)
# Make sure keras is installed properly
is_keras_available()
data <- array(rnorm(64 * 60 * 3), dim = c(64, 60, 3))
model <- keras_model_sequential()
model %>%
layer_conv_1d(
input_shape = c(60, 3), kernel_size = 8, filters = 8,
activation = "softplus", padding = "valid") %>%
layer_conv_1d(
kernel_size = 8, filters = 4, activation = "tanh",
padding = "same") %>%
layer_conv_1d(
kernel_size = 4, filters = 2, activation = "relu",
padding = "valid") %>%
layer_flatten() %>%
layer_dense(units = 64, activation = "relu") %>%
layer_dense(units = 16, activation = "relu") %>%
layer_dense(units = 3, activation = "softmax")
# Convert the model
converter <- convert(model)
# Apply the Gradient method
gradient <- run_grad(converter, data, channels_first = FALSE)
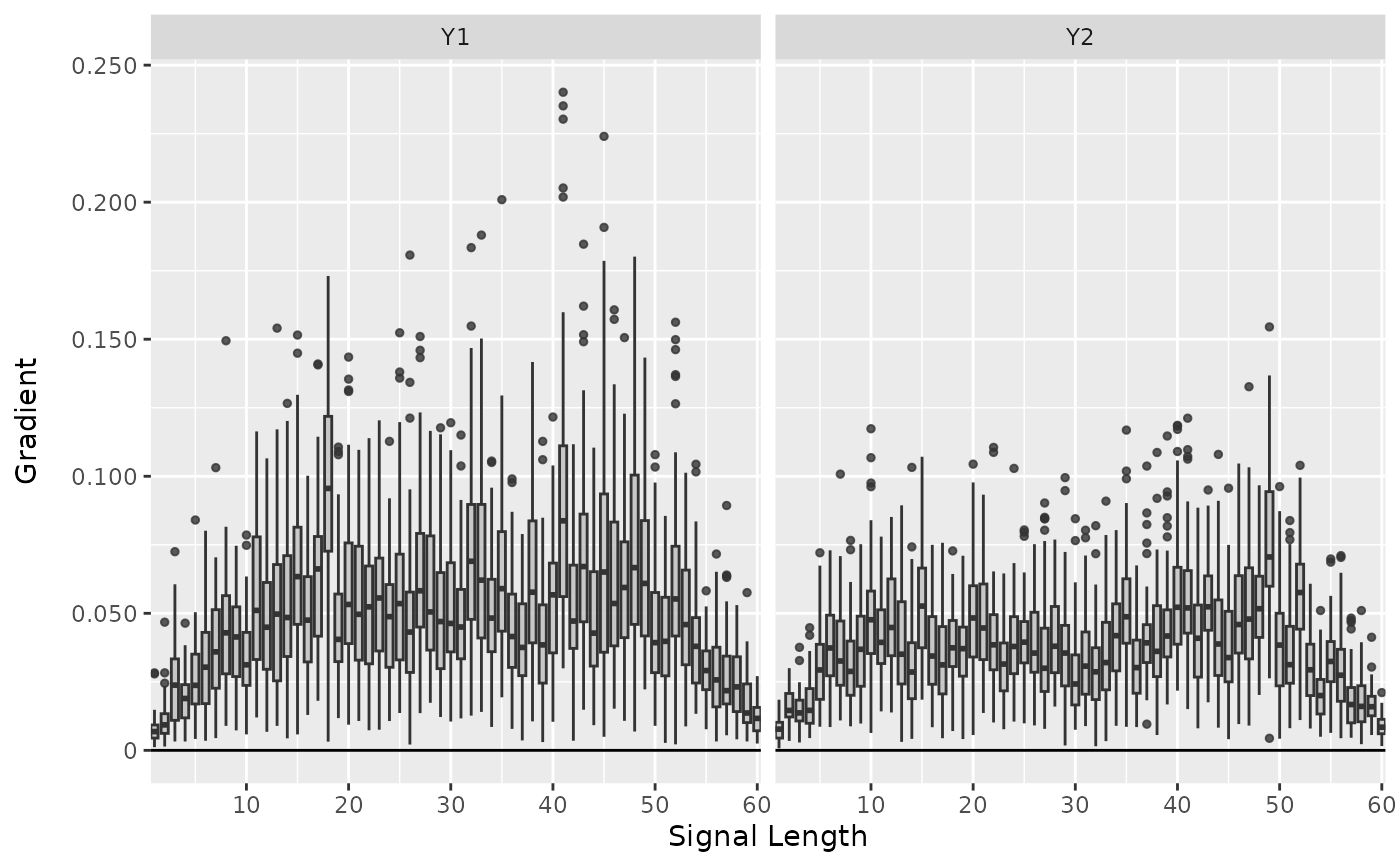
# Plot the result for the first datapoint and all classes
plot(gradient, output_idx = 1:3)
# Plot the result as boxplots for first two classes
boxplot(gradient, output_idx = 1:2)
}
# ------------------------- Example 3: Keras -------------------------------
if (require("keras") & keras::is_keras_available()) {
library(keras)
# Make sure keras is installed properly
is_keras_available()
data <- array(rnorm(64 * 60 * 3), dim = c(64, 60, 3))
model <- keras_model_sequential()
model %>%
layer_conv_1d(
input_shape = c(60, 3), kernel_size = 8, filters = 8,
activation = "softplus", padding = "valid") %>%
layer_conv_1d(
kernel_size = 8, filters = 4, activation = "tanh",
padding = "same") %>%
layer_conv_1d(
kernel_size = 4, filters = 2, activation = "relu",
padding = "valid") %>%
layer_flatten() %>%
layer_dense(units = 64, activation = "relu") %>%
layer_dense(units = 16, activation = "relu") %>%
layer_dense(units = 3, activation = "softmax")
# Convert the model
converter <- convert(model)
# Apply the Gradient method
gradient <- run_grad(converter, data, channels_first = FALSE)
# Plot the result for the first datapoint and all classes
plot(gradient, output_idx = 1:3)
# Plot the result as boxplots for first two classes
boxplot(gradient, output_idx = 1:2)
}
 #------------------------- Plotly plots ------------------------------------
if (require("plotly")) {
# You can also create an interactive plot with plotly.
# This is a suggested package, so make sure that it is installed
library(plotly)
# Result as boxplots
boxplot(gradient, as_plotly = TRUE)
# Result of the second data point
plot(gradient, data_idx = 2, as_plotly = TRUE)
}
#------------------------- Plotly plots ------------------------------------
if (require("plotly")) {
# You can also create an interactive plot with plotly.
# This is a suggested package, so make sure that it is installed
library(plotly)
# Result as boxplots
boxplot(gradient, as_plotly = TRUE)
# Result of the second data point
plot(gradient, data_idx = 2, as_plotly = TRUE)
}